1. Introduction
The ever increasing use of Internet services leads to challenges concerning transmission or storage of signals, such as image and video. In one-way communication systems, for example in digital television (DTV) broadcast (Alencar, 2009), the time lag (latency) between the signal arriving at the receiver input and being delivered as an image on the screen of a TV set, although much higher than in the old analogue TV receivers, does not constitute a critical issue. On the other hand, latency becomes a critical issue in bi-directional digital communication systems as, for example, live ex-change of medical images or mobile phone conversation. The culprit responsible for most of the latency in modern digital communication receivers is the error-correcting code (Drury, Markarian, & Pickavance, 2001). Among other improvements in future mobile systems, 5G mobile phone systems (Carlton, 2017) will employ both polar codes (Arikan, 2009) and low density parity check codes (Gallager, 2001) to reduce latency.
In this paper we make use of a recent contribution to error-correcting codes, called polar codes by Arikan (Arikan, 2009), as mentioned earlier, considering the context of image transmission.
Polar coding for image and speech transmission using successive cancellation (SC) decoding has been proved to perform better than low density parity check (LDPC) codes over AWGN channels (Zhao, Shi, & Wang, 2011; Payommai & Chamnongthai, 2013). Reference (Mishra, Sharma, & De, 2014) compares the performance of po-lar codes versus BCH codes for image transmission using the 64-QAM (quadrature amplitude modulation) orthogonal frequency division multiplexing (OFDM) system over a continuous AWGN communication chan-nel with SC decoder, for values of signal to noise ratio (Eb=N0) in the range of 5dB to 20dB, i.e., high signal to noise ratios. The concatenation of a polar code with a BCH code is also considered in (Mishra et al., 2014) and shown to improve performance in comparison with the use of polar codes, at a cost of reducing overall code rate.
Recent papers address the use of polar codes in the scenario of 60-GHz millimeter communication (Wei, Li, & Zhao, 2015) and presence of realistic impulse noise (Jin et al., 2016). For data storage applications, an algorithm with high-throughput has been introduced for SC in (Sarkis, Giard, Vardy, Thibeault, & Gross,2014), as well for successive cancellation list (SCL)
(Sarkis, Giard, Vardy, Thibeault, & Gross, 2016b). A detailed comparison in terms of complexity with SC and SCL decoders, for turbo codes and LDPC codes, can be found (Niu, Chen, Lin, & Zhang, 2014). Regarding image transmission, there are several important practical problems, such as efficient representation (i.e., efficient compression) of images aiming at reducing storage and/or easing channel bandwidth requirements. Another relevant problem is the conception and application of techniques for robust image transmission, for minimizing the annoying effects of channel errors. As a consequence, research has been done in the scenario of image compression (Hanhart, Bernardo, Pereira, G. Pinheiro, & Ebrahimi, 2015; Dhandapani & Ramachandran, 2014; Wen, Ma, & Zhao, 2014) as well as image transmission (Qazi, Shoaib, Javaid, & Asif, 2009; Liu, Wang, Chang, & Li, 2014; Abot, Olivier, Perrine, & Pousset, 2012; Sarisaray-Boluk, Gungor, Baydere, & Harmanci, 2011; Nikolakopoulos, Kandris, & Tzes, 2010; Azevedo, Madeiro, Lopes, & Lima, 2016).
Differing from the work in (Payommai & Chamnongthai, 2013) and (Mishra et al., 2014), the main goal of this paper is to investigate the quality of grey scale images transmitted through a communication system, where images are encoded with polar codes for transmission over an AWGN channel, using binary phase-shift keying (BPSK) modulation and SCL decoding, for signal to noise ratio (Eb/N0) values in the range of 0 dB to 2 dB, i.e., low signal to noise ratios. This is a relevant aspect in this paper since an investigation of the performance of SCL decoding at low signal to noise ratios in the scenario of image transmission using polar codes has not been reported earlier in the literature.
The remaining sections of this paper are organized as follows. In Section 2, polar codes, SC and SCL decoding are briefly addressed. In Section 3 the methodology employed in this investigation is presented. The results and conclusions are presented in Section 4 and Section 5, respectively.
2. Polar Codes
Polar codes are binary (N; K) linear block codes rely-ing on the appropriate choice of K bit-channels from among N bit-channels to form a codeword and thus to send information at a rate R = K/N. The other N K bit-channels are fed with zeros. The way the bit-channels are chosen is defined by the specific design employed to construct the polar code (Arikan, 2009). The basic scheme used for polar codes is shown in Fig. 1. It is worth mentioning that N = 2n, n 2 N and unless specified otherwise, all vectors, matrices, and operations on the code construction will be over the binary field GF(2).
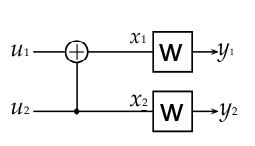
Figure 1. Basic scheme for Polar Code, for N = 2
A binary-input discrete memoryless channel (B-DMC) W is defined as W : X →Y , with input alphabet X = {0, 1} and output alphabet Y = {0, 1} with transition probabilities {W (yi|xi), xi ∈ X, yi ∈ Y }. From Fig. 1, one can write (x1, x2) = (u1 ⊕ u2, u2) where ⊕ is the modulo-2 addition. As usual, codewords are denoted as vectors x = (x1, x2, x3, . . . , xN ), which are expressed in matricial notation as
| x = u · G, | (1) |
where u = (u1, u2, u3, . . . , uN ) is the information vector and G is the N x N generator matrix for the polar code, which can be represented by the n-th Kronecker power F⊗n = F ⊗ · · · ⊗ F (n copies), with F defined as
| F = | 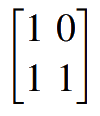 |
(2) |
The default codeword x is represented in (1), and can be rewritten using (F⊗n) with n = log2(N), as
| x = u · G = u(F⊗n). | (3) |
To represent the choice of good bit-channels and the bad bit-channels for frozen (zero) bits, consider two subsets, A and Ac, which contain the indices of the rows of the good bit-channels and bad bit-channels, respectively, from the matrix representation F⊗n. So (F⊗n)(A) is the matrix that contains the rows of non frozen bits and (F⊗n)(Ac) is the matrix that contains the rows of frozen bits. Thus, Equation (3) can, equivalently, be represented by Equation (4) as follows
| x = u (F⊗n)(A) ⊕ u(F⊗n)(Ac). | (4) |
After the encoding process, each codeword is modulated using binary phase shift keying (BPSK) and then is transmitted over a noisy channel. In this paper the AWGN channel is considered. The output of this channel can be written as yi = hi + qi, where hi = (1 − 2xi) and qi denotes a sample of a discrete-time AWGN process with zero mean and variance σ2. The transition probability PY|H (yi| hi) for the AWGN channel considered can be written as
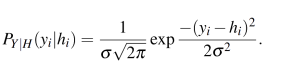 |
(5) |
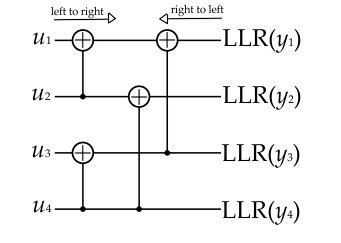
Figure 2. Decoding diagram for N = 4
The log-likelihood ratio (LLR) is obtained from Equation (5) as follows
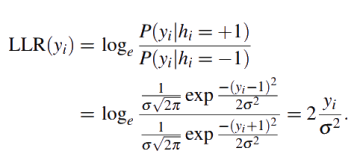 |
(6) |
With the LLR value for the i-th bit-channel obtained from Equation (6), for 1 ≤ i ≤ N, the decoding process proceeds from right to left following the same scheme used for encoding, but in a reverse way as can be seen for example in Fig. 2 for N = 4. As a final step in the decoding process, a hard-decision is made and the estimated bit ûiis propagated from left to right for intermediate decision. So the last bit decoded is used for the next bit estimation. In contrast, if the bit is wrongly estimated this error will propagate to the rest of the decoding process.
The SC decoder can be considered as a particular case of the SCL decoder (Tal & Vardy, 2015) with the number of paths equal to one. The SCL decoder considers L possible paths, L ≥ 2. When a non frozen bit decision ûi is made, a new path is created to be considered by the decoder. Anytime a split is made, the number of paths doubles, and after reaching the limit 2L, the SCL decoder discards the less probable path. This process continues until a decision on the last bit is made and the SCL decoder finally chooses the most probable path to be the sequence of ûi estimated information bits.
3. Methodology
A typical communication system used for transmitting images on the AWGN channel is shown in Fig. 3. Polar codes with block lengths N = 1024, N = 2048 and N = 4096 are used at a fixed rate R = 1/2 to investigate the quality of transmitted images when the SC decoder and the SCL decoder are employed. The images used for simulations are Lena, Peppers and Cameraman, each one having 256 × 256 pixels, 8 bits per pixel (bpp) and are represented with portable Gray map (PGM). The original images mentioned are illustrated in Fig. 4.
The pixels in a matrix that represents the original image are converted into bits. Each K bits creates the vector u with length N, where N K bits are frozen bits. After the vector u is created, it is sent to the polar encoder to generate the length N codeword x. The codeword x is modulated using BPSK and finally sent over an AWGN channel. The peak signal to noise ratio (PSNR) and the structural similarity (SSIM) (Wang, Bovik, Sheikh, & Simoncelli, 2004) are used after the image is reconstructed to evaluate the decoding performance for a range of Eb/N0 values, where Eb denotes the energy per bit and N0 is the spectral noise density, for N = 1024, N = 2048, N = 4096. The PSNR measure (in dB) is given by
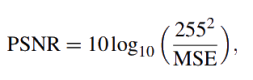 |
(7) |
where MSE denotes the mean square error, given by
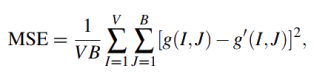 |
(8) |
where g(I, J) is the grey level of the original image g at I-th row and J-th column, V is the number of rows and B is the number of columns and g'(I, J) is the grey level of the reconstructed image g', at I-th row and J-th column, after the decoding process. The SSIM measure is given by
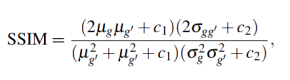 |
(9) |
where µg and µg' are the averages of images g and g' respectively, σg and σg' are the variance values from g and g' respectively, σgg' is the covariance from g and g', c1 = (k1l)2 and c2 = (k2)2l, where l is the dynamic range of pixels values, k1 = 0.01 and k2 = 0.03. These specific values of k1 and k2 were introduced in (Wang et al., 2004).
4. Computer Simulation Results
Simulation results are now presented for the image transmission scheme illustrated in Fig. 3. The quality of the reconstructed images is assessed by their corresponding PSNR and SSIM for a range of values of Eb/N0 and block lengths N. Results are presented in Fig. 5 and Fig. 6, in terms of PSNR versus Eb/N0 and SSIM versus Eb/N0 respectively, for different code block lengths using SC decoding and SCL decoding with L = 2, L = 4 and L = 8.
According to the set of PSNR (dB) versus Eb/N0 curves for the Lena image, presented in Fig. 5, one observes that the quality of the decoded image, in terms of PSNR, improves with the code block length N, for SC decoding with Eb/N0 greater than 1.2 dB.
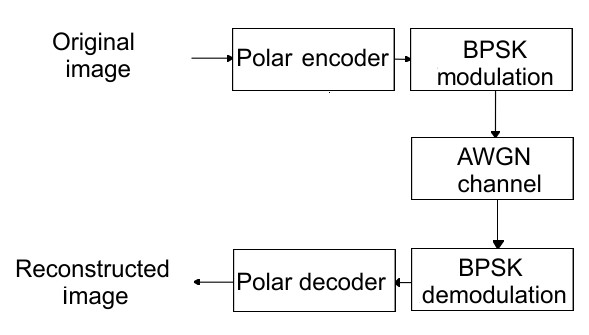
Figure 3. Block diagram of the communication system under consideration, using polar encoder, BPSK modulation, AWGN channel, BPSK demodulation, and polar decoder with SC or SCL algorithms

Figure 4. Original images having 256 x 256 pixels and 8 bpp (a) Lena, (b) Peppers, (c) Cameraman
The increase of PSNR with N is also observed for SCL decoding with L = 2, SCL with L = 4 and SCL with L = 8 for Eb/N0 greater than about 1.3 dB, 1.1 dB and 1.2 dB respectively. The reason for the increase in PSNR with code block length N relies on the channel polarization effect. Indeed, as long the as the block length increases, it follows that the number of good bit-channels (available to send information) increases and, as a consequence, a better Bhattacharyya parameter is obtained, leading to bit-error probability decrease.
The influence of the number of paths L in the quality of the decoded images is also observed in Fig. 5. Consider, for instance, Fig. 5c and Fig. 5d for Eb/N0 = 2.0 dB and N = 4096. One observes that the substitution of L = 4 by L = 8 increases PSNR from about 34 dB to about 38.4 dB; for Eb/N0 = 1.8 dB, the same substitution leads to a PSNR increase from about 30 dB to about 32.5 dB, for N = 4096.
The performance of SC decoding and SCL decoding, for different values of L, in terms of SSIM versus Eb/N0 for the Lena image may be observed in Fig. 6. Considering a range of values for Eb/N0 from approximately 1.3 dB to 2.0 dB, for SC decoding as well as for SCL decoding, with L = 2, one observes in Fig. 6a and Fig. 6b that image quality improves with code block length N for a fixed Eb/N0. As an example, for Eb/N0 = 1.8 dB and considering SCL decoding with L = 2, the substitution of N = 1024 by N = 4096 leads to an SSIM increase around 0.24, while the substitution of N = 1024 by N = 2048 leads to an SSIM increase around 0.18. One observes in Fig. 6c and Fig. 6d that, for SCL decoding with L = 4 and SCL decoding with L = 8, and a fixed Eb/N0, the highest SSIM difference obtained by substitution of N = 1024 by N = 4096 are presented for Eb/N0 ranging from around 1.5 dB to 1.8 dB.
The benefits of increasing the number of paths L, in terms of the quality of the decoded image, may be observed in Fig. 7. Considering the Lena image at Eb/N0 = 1.6 dB, visual inspection of the images depicted in Fig. 7 reveal that the subjective quality of the decoded image improves with L. Indeed the number of annoying artifacts in the decoded image decreases with L. The increasing values of PSNR and SSIM with L corroborates the improvement in image quality with increasing L. A similar behavior is observed in Fig. 8 for the Peppers image at Eb/N0 = 1.6 dB as well as in Fig. 9 for the Cameraman image at Eb/N0 = 1.6 dB. One observes in Fig. 8 that an increase in L from 4 to 8 leads to a PSNR increase from 23.12 dB to 25.39 dB and an SSIM increase from 0.8036 to 0.8209. Regarding the Cameraman image in Fig. 9, an increase in L from 4 to 8 leads to an SSIM increase from 0.8025 to 0.8276.
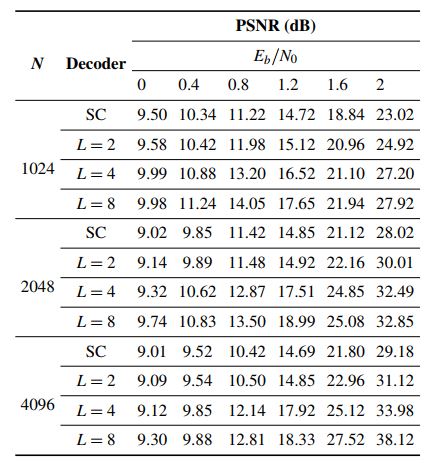
Values of PSNR and SSIM for different values of Eb/N0, using SC decoding or SCL decoding (for L = 2, L = 4 and L = 8) for N = 1024, N = 2048, and N = 4096, are presented for images Lena, Peppers, and Cameraman in Tables 1 to 4. As one observes in Table 1, for all Eb/N0 values under consideration, and for all values of N, SCL decoding with L = 2 or L = 4 or L = 8 leads to better PSNR results when compared to SC decoding. For Eb/N0 ≥ 0.4 dB and using SCL decoding, PSNR increases with L. As an example, for Eb/N0 = 1.2 dB and N = 4096, PSNR results are 14.85 dB, 17.92 dB and 18.33 dB for L = 2, L = 4 and L = 8 respectively.
Regarding SSIM results for the Lena image, presented in Table 2, the superiority of SCL decoding, with L = 2, L = 4 or L = 8, over SC decoding is observed for Eb/N0 0.4. For a fixed Eb/N0, the superiority of SCL with L = 2, L = 4 or L = 8 over SC, in terms of PSNR of the decoded Peppers image is observed in Table 3 for all values of Eb/N0, and for all values of N. For a fixed Eb/N0, the superiority of SCL decoding with L = 4 or L = 8 over SC decoding is also observed in terms of SSIM, for all values of Eb/N0 under consideration, for all values of N, as observed in Table 4. It is interesting to observe that the SSIM values for N = 4096, Eb/N0 = 2 dB are 0.9912 and 0.9928, for L = 4 and L = 8, respectively. Hence, the aforementioned SSIM results are close to the maximum SSIM, that is, SSIM=1.
Regarding PSNR results for the Cameraman image, one observes in Table 4 that, for a fixed Eb/N0, a better image quality in terms of PSNR is obtained if SC decoding is substituted by SCL decoding with L = 2 or L = 4 or L = 8, for all values of N. As an example, for Eb/N0 = 1.6 dB, PSNR increases from 22.51 to 25.62 dB if SC decoding is replaced by SCL decoding, for L = 8, with N = 4096. The benefits of using SCL decoding in substitution to SC decoding is clearly observed in Table 4, for the Cameraman image, mainly for L = 4 and L = 8.
Improvement on image quality transmitted through an AWGN channel at low signal to noise ratios has been verified by means of computer simulations employing polar codes, with the substitution of classical successive cancellation (SC) decoding by successive cancellation list (SCL) decoding. Polar codes showed to be robust for operation at low signal to noise ratios. The results are presented in terms of PSNR versus Eb/N0 and SSIM versus Eb/N0, for code block lengths of 1024, 2048 and 4096 bits, employing SC decoding and SCL decoding (L = 2, L = 4, L = 8), and are reflected in visual inspection of the images Lena, Peppers and Cameraman. The advantage in using SCL decoding (L = 2, L = 4, L = 8) instead of the SC decoding algorithm was verified in all cases investigated, for Eb/N0 0.8 dB and the quality of the decoded images improves but with diminishing incremental gains as L increases. For completeness sake, for future work on this topic it is suggested to investigate the performance using fast and simplified SCL (Hashemi, Condo, & Gross, 2016, 2017; Sarkis, Giard, Vardy, Thibeault, & Gross, 2016a) and using other decoding algorithms, such as belief propagation decoding, for example, to replace SC decoding and SCL decoding.
Table 1. PSNR values for a range of Eb/N0 values and polar codes (1024, 512), (2048, 1024) and (4096, 2048), for the Lena image
5. Conclusion
Improvement on image quality transmitted through an AWGN channel at low signal to noise ratios has been verified by means of computer simulations employing polar codes, with the substitution of classical successive cancellation (SC) decoding by successive cancellation list (SCL) decoding. Polar codes showed to be robust for operation at low signal to noise ratios.
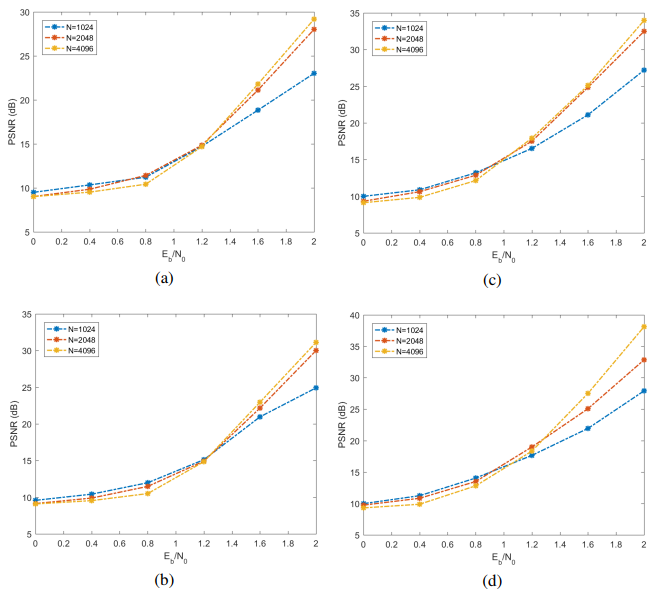
Figure 5. PSNR (dB) versus Eb/N0 for Lena image using SC and SCL decoding, with polar codes (1024, 512), (2048, 1024) and (4096, 2048) for different values of L. (a) SC, (b) SLC for L = 2, (c) SLC for L = 4 and (d) SLC for L = 8
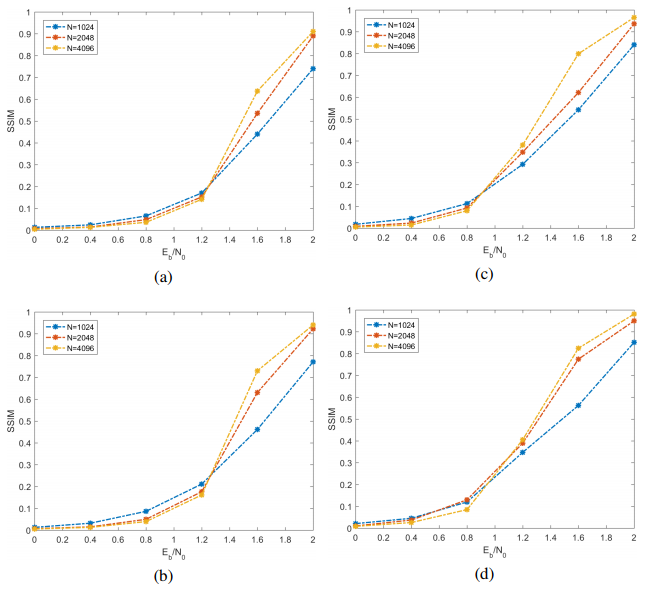
Figure 6. SSIM versus Eb/N0 for Lena image using SC or SCL decoding, with polar codes (1024, 512), (2048, 1024) and (4096, 2048) for different values of L. (a) SC, (b) SLC for L = 2, (c) SLC for L = 4 and (d) SLC for L = 8

Figure 7. Lena image using SC or SCL decoding with different values of L for the polar code (4096, 2048), at Eb/N0 = 1.6dB. (a) SC with PSNR = 21.79 dB and SSIM = 0.6411, (b) L = 4 with PSNR = 25.83 dB and SSIM = 0.8210, (c) L = 8 with PSNR = 27.30 dB and SSIM = 0.8641
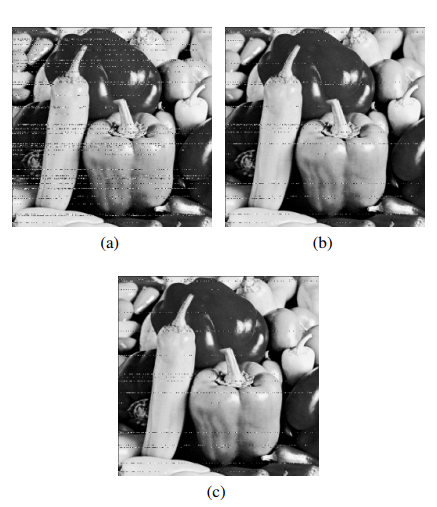
Figure 8. Peppers image using SC or SCL decoding for the polar code (4096, 2048) and different values of L, at Eb/N0 = 1.6 dB. (a) SC with PSNR = 20.01 dB and SSIM = 0.6857, (b) L = 4 with PSNR = 23.12 dB and SSIM = 0.8036, (c) L = 8 with PSNR = 25.39 dB and SSIM = 8209

Figure 9. Cameraman image using SC or SCL decoding for the polar code (4096, 2048) and different values of L, at Eb/N0 = 1.6 dB. (a) SC with PSNR = 21.88 dB and SSIM = 0.6489, (b) L = 4 with PSNR = 25.50 dB and SSIM = 0.8025, (c) L = 8 with PSNR = 26.14 dB and SSIM = 0.8276
Table 2. SSIM values for a range of Eb/N0 values and polar codes (1024, 512), (2048, 1024) and (4096, 2048), for the Lena image
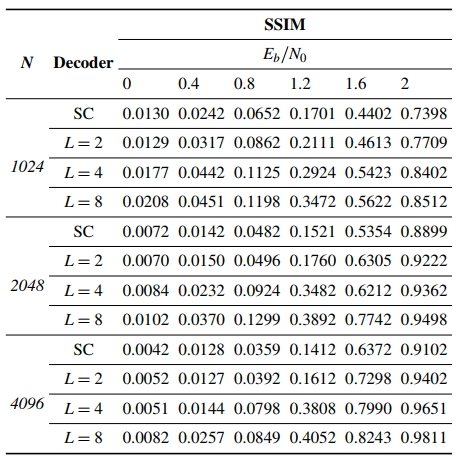
Table 3. SPSNR values for a range of Eb/N0 values and polar codes (1024, 512), (2048, 1024) and (4096, 2048), for the Peppers image
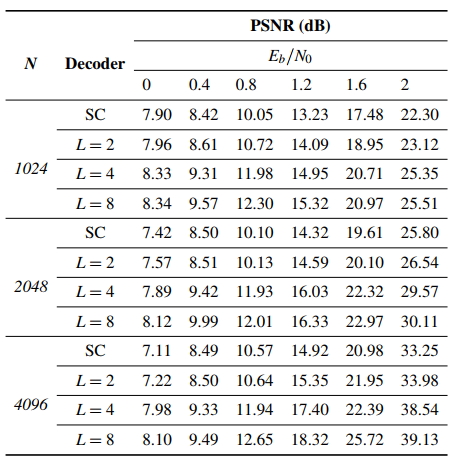
The results are presented in terms of PSNR versus Eb/N0 and SSIM versus Eb/N0, for code block lengths of 1024, 2048 and 4096 bits, employing SC decoding and SCL decoding (L = 2, L = 4, L = 8), and are reflected in visual inspection of the images Lena, Peppers and Cameraman. The advantage in using SCL decoding (L = 2, L = 4, L = 8) instead of the SC decoding algorithm was verified in all cases investigated, for Eb/N0 0.8 dB and the quality of the decoded images improves but with diminishing incremental gains as L increases. For completeness sake, for future work on this topic it is suggested to investigate the performance using fast and simplified SCL (Hashemi, Condo, & Gross, 2016, 2017; Sarkis, Giard, Vardy, Thibeault, & Gross, 2016a) and using other decoding algorithms, such as belief propagation decoding, for example, to replace SC decoding and SCL decoding.
Acknowledgements
A. M. A. Garcia would like to thank the Brazilian Ministry of Education Agency - CAPES for partially funding this research. V. C. da Rocha Jr. acknowledges partial support by the Brazilian National Council for Scientific and Technological Development - CNPq under project no. 307467/2015-5. Francisco Madeiro acknowledges partial support by the Brazilian National Council for Scientific and Technological Development - CNPq under project no. 310447/2014-3.
References
Abot, J., Olivier, C., Perrine, C., & Pousset, Y. (2012, November). A link adaptation scheme optimized for wireless JPEG 2000 transmission over realistic MIMO systems. Signal Processing: Image Communication, 27(10), 1066–1078. doi: 10.1016/j.image.2012.08.003
Alencar, M. S. (2009). Digital television systems. New York, NY, USA: Cambridge University Press.
Arikan, E. (2009, July). Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Transactions on Information Theory, 55(7), 3051-3073. doi: 10.1109/TIT.2009.2021379
Azevedo, R. A., Madeiro, F., Lopes, W. T. A., & Lima, E. A. O. (2016, March). A quasi random symbol interleaving technique applied to image transmission by noisy channels. IEEE Latin America Transactions, 14(3), 1078-1085. doi: 10.1109/TLA.2016.7459582
Carlton, A. (2017, March). 5G and future mobile. Networkworld, http://www.networkworld.com/article/3151866/mobile-wireless/surprise-polar-codes-are-coming-in-from-the-cold.htm.
Dhandapani, V., & Ramachandran, S. (2014). Area and power efficient DCT architecture for image compression. EURASIP Journal on Advances in Signal Processing(1), 2014:180. doi: 10.1186/1687-6180-2014-180
Drury, G., Markarian, G., & Pickavance, K. (2001). Coding and modulation for digital television. London, UK: Kluwer Academic Publishers.
Gallager, R. G. (2001). Low density parity check codes. Cambridge, Massachusetts, USA: MIT Press.
Hanhart, P., Bernardo, M. V., Pereira, M., G. Pinheiro, A. M., & Ebrahimi, T. (2015). Benchmarking of objective quality metrics for HDR image quality assessment. EURASIP Journal on Image and Video Processing(1), 2015:39. doi: 10.1186/s13640-015-0091-4
Hashemi, S. A., Condo, C., & Gross, W. J. (2016). A fast polar code list decoder architecture based on sphere decoding. IEEE Transactions on Circuits and Systems I: Regular Papers, 63(12), 2368– 2380.
Hashemi, S. A., Condo, C., & Gross, W. J. (2017). Fast and flexible successive-cancellation list decoders for polar codes. IEEE Transactions on Signal Processing, 65(21), 5756–5769.
Jin, L., Li, Y., Zhao, C., Wei, Z., Li, B., & Shi, J.
(2016). Cascading polar coding and lt coding for radar and sonar networks. EURASIP Journal on Wireless Communications and Networking(1), 2016:254. doi: 10.1186/s13638-016-0748-4
Liu, L., Wang, A., Chang, C.-C., & Li, Z. (2014, January). A novel real-time and progressive secret image sharing with flexible shadows based on compressive sensing. Signal Processing: Image Communication, 29(1), 128–134. doi: 10.1016/j.image.2013.10.003
Mishra, A., Sharma, K., & De, A. (2014, January). Quality image transmission through awgn channel using polar codes. International Journal of Computer Science and Telecommunication, 5.
Nikolakopoulos, G., Kandris, D., & Tzes, A. (2010). Adaptive compression of slowly varying images transmitted over wireless sensor networks. Sensors, 10(8), 7170. doi: 10.3390/s100807170
Niu, K., Chen, K., Lin, J., & Zhang, Q. T. (2014, July). Polar codes: Primary concepts and practical decoding algorithms. IEEE Communications Magazine, 52(7), 192-203. doi: 10.1109/MCOM.2014.6852102
Payommai, T., & Chamnongthai, K. (2013, Nov). Performance of polar code for image transmission. In 2013 international symposium on intelligent signal processing and communication systems (p. 450-453). doi: 10.1109/ISPACS.2013.6704592
Qazi, S. A., Shoaib, M., Javaid, U., & Asif, S. (2009). A comparative analysis of LDPC decoders for image transmission over AWGN channel. In Proceedings of the 7th international conference on frontiers of information technology (pp. 4:1–4:5). New York, NY, USA: ACM. doi: 10.1145/1838002.1838007
Sarisaray-Boluk, P., Gungor, V. C., Baydere, S., & Harmanci, A. E. (2011, September). Quality aware image transmission over underwater multimedia sensor networks. Ad Hoc Networks., 9(7), 1287– 1301. doi: 10.1016/j.adhoc.2011.02.007
Sarkis, G., Giard, P., Vardy, A., Thibeault, C., & Gross, W. J. (2014, May). Fast polar decoders: Algorithm and implementation. IEEE Journal on Selected Areas in Communications, 32(5), 946-957. doi: 10.1109/JSAC.2014.140514
Sarkis, G., Giard, P., Vardy, A., Thibeault, C., & Gross, W. J. (2016a). Fast list decoders for polar codes. IEEE Journal on Selected Areas in Communications, 34(2), 318–328.
Sarkis, G., Giard, P., Vardy, A., Thibeault, C., & Gross, W. J. (2016b, Feb). Fast list decoders for polar codes. IEEE Journal on Selected Areas in Communications, 34(2), 318-328. doi: 10.1109/JSAC.2015.2504299
Tal, I., & Vardy, A. (2015, May). List decoding of polar codes. IEEE Transactions on Information Theory, 61(5), 2213-2226. doi: 10.1109/TIT.2015.2410251
Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004, April). Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600-612. doi: 10.1109/TIP.2003.819861
Wei, Z., Li, B., & Zhao, C. (2015). On the polar code for the 60-GHz millimeter-wave systems. EURASIP Journal on Wireless Communications and Networking. doi: 10.1186/s13638-015-0264-y
Wen, J., Ma, C., & Zhao, J. (2014). FIVQ algorithm for interference hyper-spectral image compression. Optics Communications, 322, 97-104. doi: 10.1016/j.optcom.2014.02.016
Zhao, S., Shi, P., & Wang, B. (2011, Nov). Polar codes and its application in speech communication. In 2011 international conference on wireless communications and signal processing (wcsp) (p. 1-4). doi: 10.1109/WCSP.2011.6096731
